异或求和式

参考于：https://blog.csdn.net/ECNU_LZJ/article/details/72853774?utm_medium=distribute.pc_relevant.none-task-blog-OPENSEARCH-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-1.nonecase

题目

给定长度为n的序列A[i]，求所有A[i] xor A[j] (i

输入

第一行一个整数N
接下来N行，第i行为A[i]

输出

所需的值

样例输入

3
7 3 5

样例输出

12

样例解释

7 xor 3+3 xor 5+7 xor 5 = 4+6+2 = 12

题解

异或：C++中即为 ^ 运算符
0^0=0 , 0^1=1 ,1^0=1, 1^1=0

数字都化成二进制：7:111, 3:011, 5:101
异或具有交换律，也就是说只要能够使得任意两个数字都异或一次，就没有必要每次用前面的数字异或后面的数字。这启发我们不关注异或的顺序，而是关注结果。
易知：a个1，b个0两两异或的结果肯定是a*b个1，其余都是0。
三个数字的最低位分别是1,1,1，也就是三个1。那么最低位异或的结果一定是零个1，三个0，相加为0。
次低位分别是1,1,0，也就是两个1一个0。那么次低位异或的结果一定是两个1，一个0，相加为2。
最高位分别是1,0,1，也就是两个1一个0。那么最高位异或的结果一定是两个1，一个0，相加为2。
所以最后的答案应该是

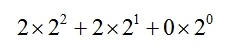
代码如下：

#include 
#include 
using namespace std;
long long b[50]={0};
int main()
{
    int n;
    scanf("%d",&n);
    long long a;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a);
        int cnt=0;
        while(a)
        {
            cnt++;
            if(a%2==1)
            {
                b[cnt]++;
            }
            a=a/2;
        }
    }
    long long sum=0;
    for(int i=0;i<=31;i++)
    {
        sum=sum+(1<